NumPyは、Pythonで科学計算を行うための基本的なライブラリであり、高性能な多次元配列オブジェクトを提供します。NumPyは、数値計算やデータ分析、機械学習などの分野で広く利用されています。
Numpyとは
NumPy(Numerical Python)は、Pythonで科学計算を行うためのライブラリです。多次元配列オブジェクトであるndarrayや、高度な数学関数、乱数生成機能、線形代数、フーリエ変換などを提供します。
インストール
まず、NumPyを使用するには、ライブラリをインストールする必要があります。以下のコマンドを使用します:
pip install numpy基本的な使い方
NumPyを使用するためには、import文を使ってインポートします。
import numpy as np配列の作成
NumPyの基本的な機能は、配列(ndarray)の作成です。配列はリストやタプルから作成できます。
import numpy as np
# リストから1次元配列を作成
array1 = np.array([1, 2, 3, 4, 5])
print("1次元配列:", array1)
# リストのリストから2次元配列を作成
array2 = np.array([[1, 2, 3], [4, 5, 6]])
print("2次元配列:\n", array2)結果
1次元配列: [1 2 3 4 5]
2次元配列:
[[1 2 3]
[4 5 6]]配列の操作
配列の操作には、スライシング、形状変更、結合、分割などがあります。
import numpy as np
# リストから1次元配列を作成
array1 = np.array([1, 2, 3, 4, 5])
print("1次元配列:", array1)
# リストのリストから2次元配列を作成
array2 = np.array([[1, 2, 3], [4, 5, 6]])
print("2次元配列:\n", array2)
# 配列のスライシング
print("配列の一部:", array1[1:4])
# 配列の形状変更
array3 = np.reshape(array2, (3, 2))
print("形状変更:\n", array3)
# 配列の結合
array4 = np.concatenate((array1, array1))
print("結合された配列:", array4)
# 配列の分割
array5, array6 = np.split(array4, 2)
print("分割された配列1:", array5)
print("分割された配列2:", array6)結果
1次元配列: [1 2 3 4 5]
2次元配列:
[[1 2 3]
[4 5 6]]
配列の一部: [2 3 4]
形状変更:
[[1 2]
[3 4]
[5 6]]
結合された配列: [1 2 3 4 5 1 2 3 4 5]
分割された配列1: [1 2 3 4 5]
分割された配列2: [1 2 3 4 5]乱数の生成
NumPyには乱数生成機能があり、さまざまな分布に従う乱数を生成できます。
import numpy as np
# 一様分布に従う乱数
random_array1 = np.random.rand(3, 3)
print("一様分布に従う乱数:\n", random_array1)
# 正規分布に従う乱数
random_array2 = np.random.randn(3, 3)
print("正規分布に従う乱数:\n", random_array2)
# 整数の乱数
random_array3 = np.random.randint(1, 10, size=(3, 3))
print("整数の乱数:\n", random_array3)結果
一様分布に従う乱数:
[[0.69542326 0.40028482 0.65790097]
[0.86880309 0.17099388 0.80661965]
[0.18869321 0.66311483 0.19259946]]
正規分布に従う乱数:
[[-0.24304776 0.11608699 -0.73989509]
[-1.85696767 -0.39619907 -1.77964674]
[ 0.15981647 1.08657431 1.21873543]]
整数の乱数:
[[5 4 6]
[8 4 9]
[6 6 9]]線形代数
NumPyは、線形代数に関連する多くの関数を提供しています。例えば、行列積、行列の逆、行列式、固有値などです。
import numpy as np
# 行列の積
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])
product = np.dot(matrix1, matrix2)
print("行列の積:\n", product)
# 行列の逆
inverse = np.linalg.inv(matrix1)
print("行列の逆:\n", inverse)
# 行列式
determinant = np.linalg.det(matrix1)
print("行列式:", determinant)
# 固有値
eigenvalues, eigenvectors = np.linalg.eig(matrix1)
print("固有値:", eigenvalues)
print("固有ベクトル:\n", eigenvectors)結果
行列の積:
[[19 22]
[43 50]]
行列の逆:
[[-2. 1. ]
[ 1.5 -0.5]]
行列式: -2.0000000000000004
固有値: [-0.37228132 5.37228132]
固有ベクトル:
[[-0.82456484 -0.41597356]
[ 0.56576746 -0.90937671]]実例
例題1: 配列の統計量計算
以下の例では、配列の平均、中央値、標準偏差を計算します。
import numpy as np
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
mean = np.mean(data)
median = np.median(data)
std_dev = np.std(data)
print("平均:", mean)
print("中央値:", median)
print("標準偏差:", std_dev)結果
平均: 5.5
中央値: 5.5
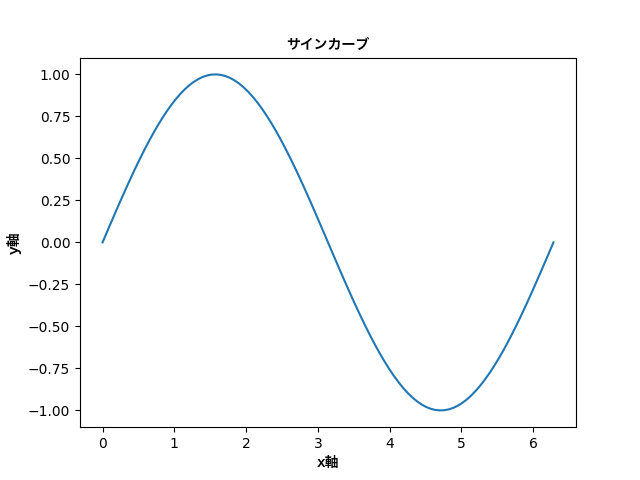
標準偏差: 2.8722813232690143例題2: サインカーブのプロット
以下の例では、NumPyを使用してサインカーブを生成し、Matplotlibを使用してプロットします。
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi, 100)
y = np.sin(x)
plt.plot(x, y)
plt.xlabel("x軸")
plt.ylabel("y軸")
plt.title("サインカーブ")
plt.show()