SymPyは、Pythonでシンボリック計算を行うためのオープンソースライブラリです。数式の解析、操作、解法を自動化するための強力なツールであり、数値計算にとどまらず、数式自体を操作する能力を提供します。以下に、SymPyの特徴と実用例を説明します。
SymPyの特徴
シンボリック計算
SymPyは、数式のシンボリック計算をサポートしており、数値ではなく変数や数式そのものを扱います。これにより、数式の簡約、微分、積分、方程式の解法などが可能です。
数式操作の豊富な機能
SymPyは、数式の展開、因数分解、単純化、展開など、さまざまな数式操作を行うための関数を提供します。
数式の可視化
SymPyは、数式をLaTeXやMathML形式で出力でき、数式の視覚化やレポートの作成が容易です。
互換性
SymPyは、他のPythonライブラリと簡単に統合でき、科学計算やデータ解析のワークフローにシームレスに組み込むことができます。
例題1: 基本的なシンボリック計算
まず、SymPyを使用して基本的なシンボリック計算を行う方法を示します。
import sympy as sp
# シンボルの定義
x, y = sp.symbols('x y')
# 数式の定義
expr = x**2 + 2*x + 1
# 数式の展開
expanded_expr = sp.expand(expr)
print("展開された数式:", expanded_expr)
# 数式の因数分解
factored_expr = sp.factor(expanded_expr)
print("因数分解された数式:", factored_expr)
# 数式の微分
diff_expr = sp.diff(expr, x)
print("微分された数式:", diff_expr)
# 数式の積分
integrated_expr = sp.integrate(expr, x)
print("積分された数式:", integrated_expr)結果
開された数式: x**2 + 2*x + 1
因数分解された数式: (x + 1)**2
微分された数式: 2*x + 2
積分された数式: x**3/3 + x**2 + xこのコードでは、数式の展開、因数分解、微分、積分を行っています。SymPyのexpand、factor、diff、integrate関数を使用して、簡単に数式操作が可能です。
例題2: 方程式の解法
次に、SymPyを使用して方程式を解く方法を示します。
import sympy as sp
# シンボルの定義
x = sp.symbols('x')
# 方程式の定義
equation = sp.Eq(x**2 - 4, 0)
# 方程式の解法
solutions = sp.solve(equation, x)
print("方程式の解:", solutions)結果
方程式の解: [-2, 2]このコードでは、二次方程式 x2−4=0x^2 – 4 = 0x2−4=0 を解いています。sp.Eq関数で方程式を定義し、sp.solve関数で解を求めます。
例題3: 行列の操作
SymPyを使用して行列の操作を行う方法を示します。
import sympy as sp
# 行列の定義
matrix = sp.Matrix([[1, 2], [3, 4]])
# 行列の逆行列
inverse_matrix = matrix.inv()
print("逆行列:")
sp.pprint(inverse_matrix)
# 行列の固有値と固有ベクトル
eigenvals = matrix.eigenvals()
eigenvects = matrix.eigenvects()
print("固有値:", eigenvals)
print("固有ベクトル:", eigenvects)結果
逆行列:
⎡-2 1 ⎤
⎢ ⎥
⎣3/2 -1/2⎦
固有値: {5/2 - sqrt(33)/2: 1, 5/2 + sqrt(33)/2: 1}
固有ベクトル: [(5/2 - sqrt(33)/2, 1, [Matrix([[-sqrt(33)/6 - 1/2],[ 1]])]), (5/2 + sqrt(33)/2, 1, [Matrix([[-1/2 + sqrt(33)/6],[ 1]])])]このコードでは、行列の逆行列を計算し、固有値と固有ベクトルを求めています。Matrixオブジェクトを使用して行列を定義し、invメソッドで逆行列を計算し、eigenvalsおよびeigenvectsメソッドで固有値と固有ベクトルを求めます。
例題4: 数式の可視化
SymPyを使用して数式を可視化する方法を示します。
import sympy as sp
# シンボルの定義
x = sp.symbols('x')
# 数式の定義
expr = sp.sin(x) + sp.cos(x)
# 数式のLaTeX形式の出力
latex_expr = sp.latex(expr)
print("LaTeX形式の数式:", latex_expr)
# 数式のプロット
sp.plot(expr, (x, -10, 10), title='Plot of sin(x) + cos(x)')結果
LaTeX形式の数式: \sin{\left(x \right)} + \cos{\left(x \right)}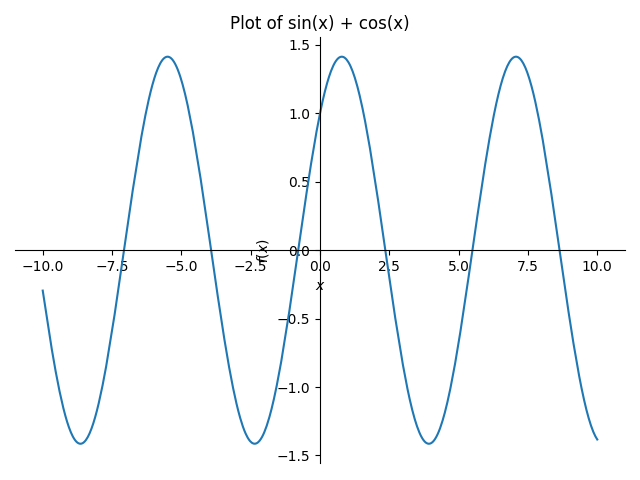
このコードでは、数式 sin(x)+cos(x)\sin(x) + \cos(x)sin(x)+cos(x) を定義し、そのLaTeX形式を出力し、プロットを作成しています。sp.latex関数で数式をLaTeX形式に変換し、sp.plot関数で数式のグラフを表示します。
結論
SymPyは、Pythonでシンボリック計算を行うための強力なツールであり、数式の操作、解法、可視化を容易にします。SymPyを活用することで、数式に関する複雑な操作を効率的に行い、研究や教育における数理解析の精度と効率を向上させることができます。SymPyの多様な機能により、数式操作のあらゆるニーズに対応できる点も大きな魅力です。

