量子コンピューティングは、従来のコンピュータでは解決が困難な問題を解決するための新しい計算パラダイムです。この分野におけるフォノニッククリスタルの進化は、量子情報の保存、伝送、および操作における重要なブレークスルーをもたらしています。フォノニッククリスタルは、音波(フォノン)を制御するための人工構造物であり、量子コンピュータの性能向上に寄与しています。目次
フォノニッククリスタルの基本原理
フォノニッククリスタルは、音波の伝播を制御するための周期的な構造を持つ材料です。これにより、特定の周波数帯域での音波の伝播を遮断するバンドギャップを形成します。この特性は、音波のフィルタリングやガイドに利用され、量子コンピューティングにおいても重要な役割を果たします。
量子コンピューティングにおけるフォノニッククリスタルの進化
量子情報の保存と伝送
フォノニッククリスタルは、量子ビット(キュービット)の情報を保存し、伝送するための媒体として利用されます。フォノンは量子状態を保持し、他のキュービットと相互作用することができます。
フォノンバンドギャップの利用
フォノニッククリスタルのバンドギャップ特性を利用して、特定の周波数帯域でのフォノンの伝播を遮断し、不要な振動やノイズを排除することができます。これにより、量子ビットのコヒーレンス時間が延長され、量子計算の精度が向上します。
高精度な制御
フォノニッククリスタルの精密な構造設計により、フォノンの伝播経路を高精度で制御できます。これにより、量子ビット間の相互作用を制御し、量子ゲート操作の精度を向上させることが可能です。
例題:フォノニッククリスタルを用いた量子メモリの設計
以下に、フォノニッククリスタルを利用した量子メモリの設計例を示します。この例では、フォノニッククリスタルのバンドギャップ特性を利用して、量子ビットの情報を保存する方法を紹介します。
構造の設計
フォノニッククリスタル量子メモリは、周期的に配置された異なる材料から構成され、特定の周波数帯域でフォノンの伝播を遮断します。
シミュレーション
フォノニッククリスタルの特性をシミュレーションするために、有限要素法(FEM)を使用します。以下は、Pythonで有限要素解析を行うための簡単なコード例です。
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eigh
# 材料の特性
rho_A = 7800 # 材料Aの密度 (kg/m^3)
rho_B = 2700 # 材料Bの密度 (kg/m^3)
c_A = 5000 # 材料Aの音速 (m/s)
c_B = 3000 # 材料Bの音速 (m/s)
# フォノニッククリスタルのパラメータ
a = 1e-3 # 格子定数 (m)
N = 10 # 単位セルの数
# 質量と剛性のマトリックスの定義
M = np.zeros((2*N, 2*N))
K = np.zeros((2*N, 2*N))
for i in range(N):
M[2*i, 2*i] = rho_A * a
M[2*i+1, 2*i+1] = rho_B * a
K[2*i, 2*i] = c_A**2 * a
K[2*i+1, 2*i+1] = c_B**2 * a
# 固有値解析
w2, v = eigh(K, M)
f = np.sqrt(w2) / (2 * np.pi)
# 結果のプロット
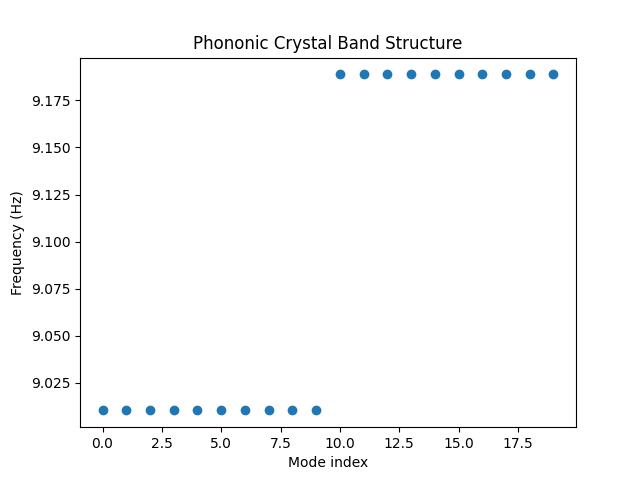
plt.plot(f, 'o')
plt.xlabel('Mode index')
plt.ylabel('Frequency (Hz)')
plt.title('Phononic Crystal Band Structure')
plt.show()このコードでは、材料AとBの密度と音速を設定し、フォノニッククリスタルの格子定数と単位セルの数を定義しています。質量マトリックス(M)と剛性マトリックス(K)を構築し、固有値解析を行ってフォノニッククリスタルのバンド構造を計算します。結果として、モードインデックスに対する周波数をプロットしています。
量子ゲートの実装
フォノニッククリスタルを用いた量子ゲートの実装は、量子ビット間の相互作用を制御するために重要です。以下のコード例では、フォノニッククリスタルの特性を利用して、簡単な量子ゲート操作をシミュレートします。
import numpy as np
from scipy.linalg import expm
# 量子ビットの初期状態
qubit_state = np.array([1, 0]) # |0> 状態
# ハミルトニアン行列の定義
H = np.array([[0, 1], [1, 0]]) # Xゲート
# 時間発展のシミュレーション
def time_evolution(H, state, t):
U = expm(-1j * H * t)
return U @ state
# 時間tでの量子状態を計算
t = np.pi / 2
final_state = time_evolution(H, qubit_state, t)
print("Initial state:", qubit_state)
print("Final state after applying X gate:", final_state)このコードでは、ハミルトニアン行列を定義し、時間発展のシミュレーションを行っています。初期状態が|0>の量子ビットに対してXゲートを適用し、最終状態を計算しています。
Initial state: [1 0]
Final state after applying X gate: [0.+0.j 0.-1.j]結論
量子コンピューティングにおけるフォノニッククリスタルの進化は、音波の伝播を精密に制御することで、量子情報の保存、伝送、および操作において重要な役割を果たしています。フォノニッククリスタルのバンドギャップ特性や高精度な制御技術は、量子ビットのコヒーレンス時間の延長や量子ゲート操作の精度向上に寄与します。将来的には、フォノニッククリスタルを活用した新たな量子コンピューティング技術の開発が期待されています。




コメント